Week 2: Spiral of Theodorus


This week the Spiral of Theodorus can be used to enhance understanding of the pythagorean theorem, right triangles, pi, and more. The spiral goes by many names (square root, Pythagorean, or Einstein Spiral) and approximates the Archimedean Spiral.
Instructions:
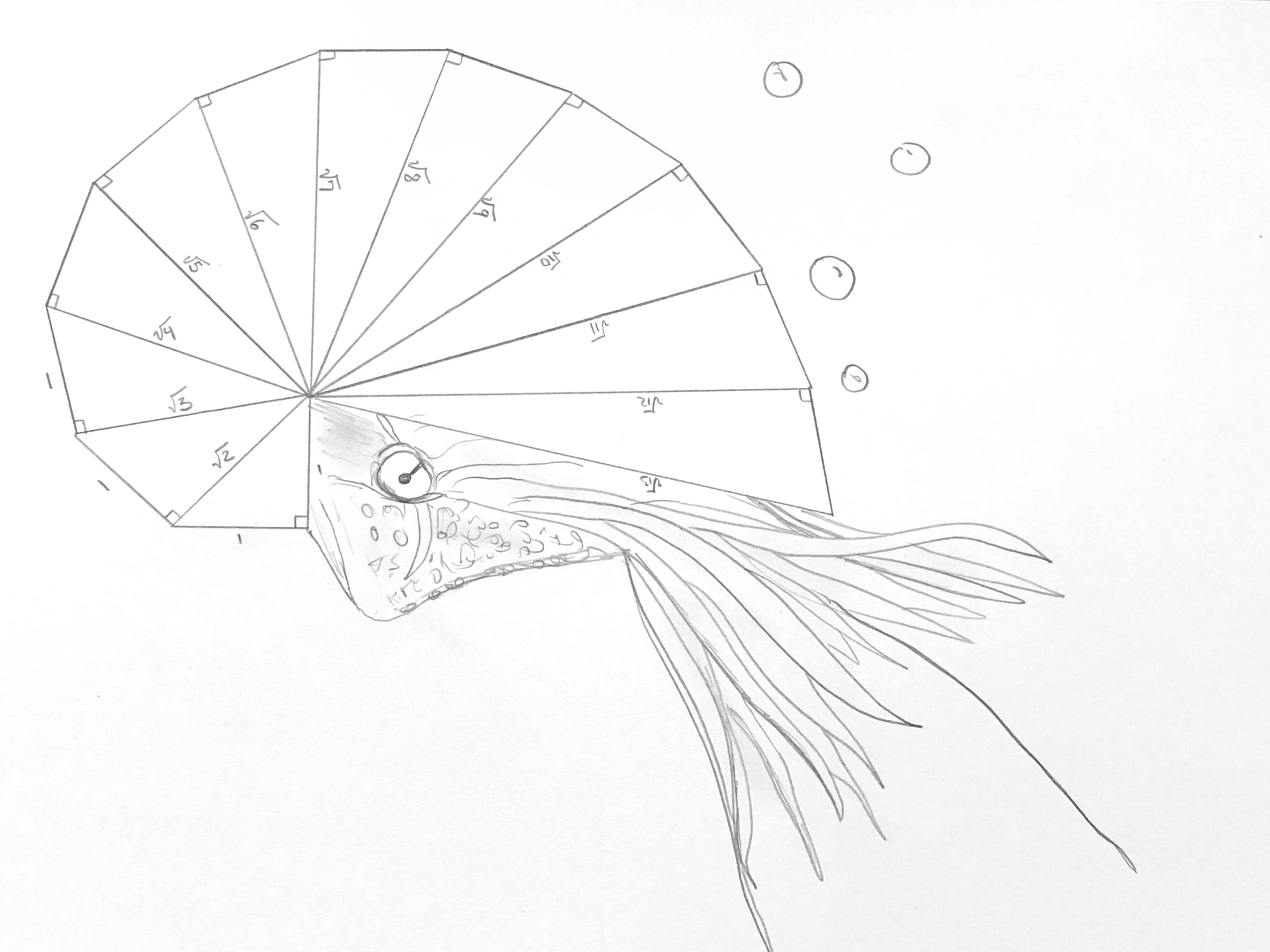
1.) Create a right isosceles triangle where the sides that are the same measure 1 unit (I used inches).
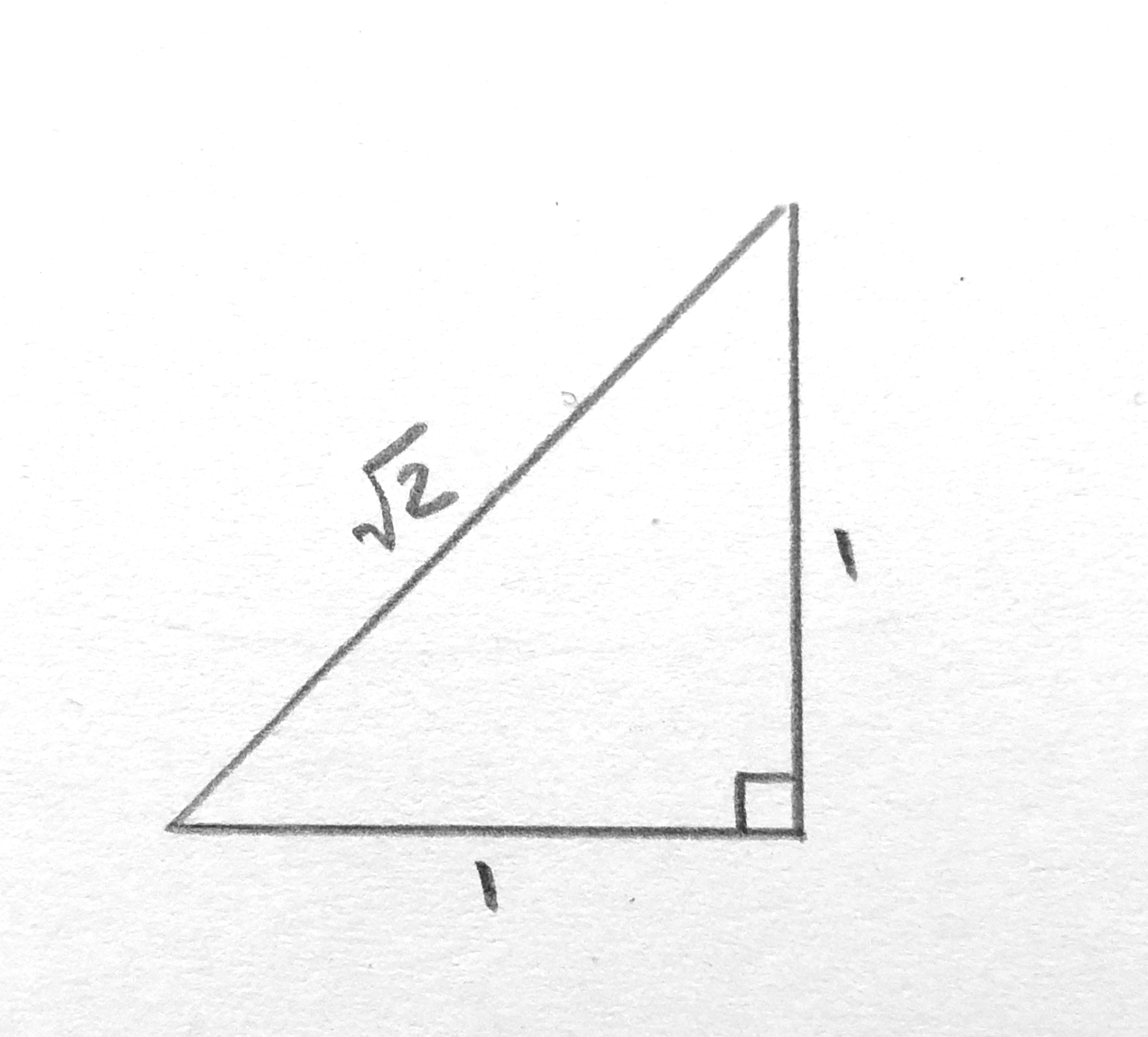
2.) Add a 1 unit line segment perpendicular to the hypotenuse of your first triangle and then connect it to create another right triangle.
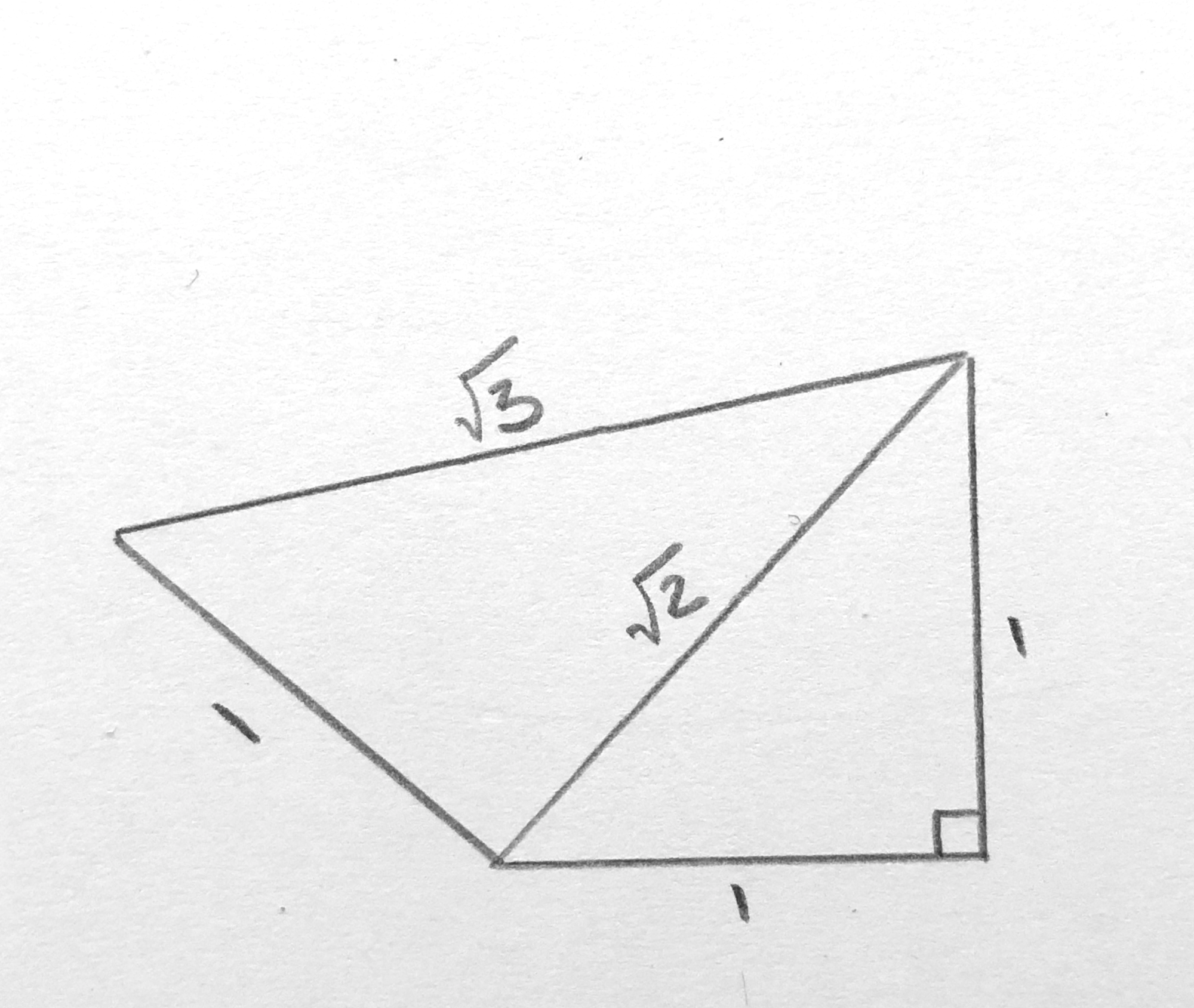
3.) Add another 1 unit line segment to the hypotenuse created in step 3 and connect it to the center to create another triangle.
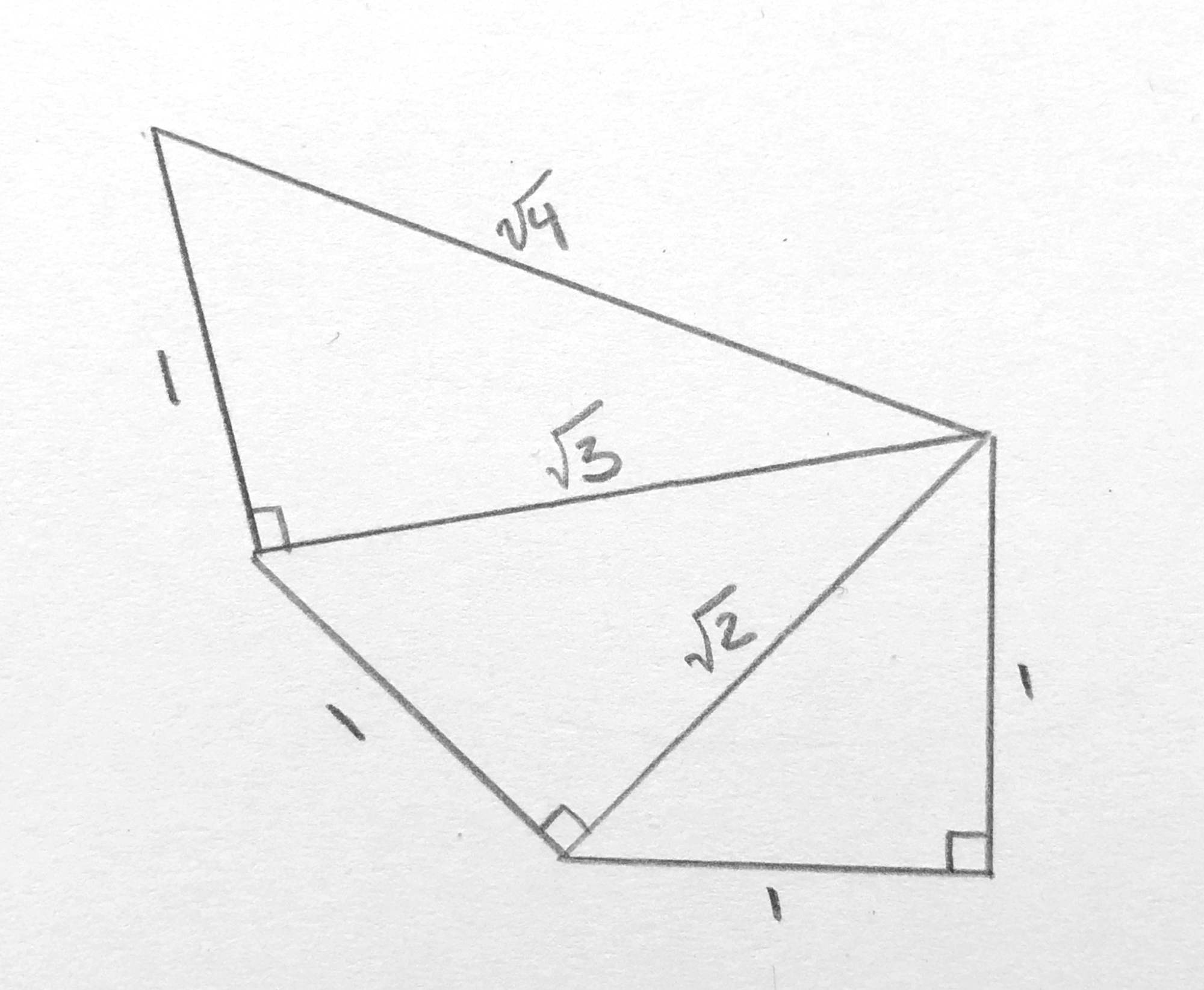
4.) Repeat step 3 as many times as you wish to expand your spiral.
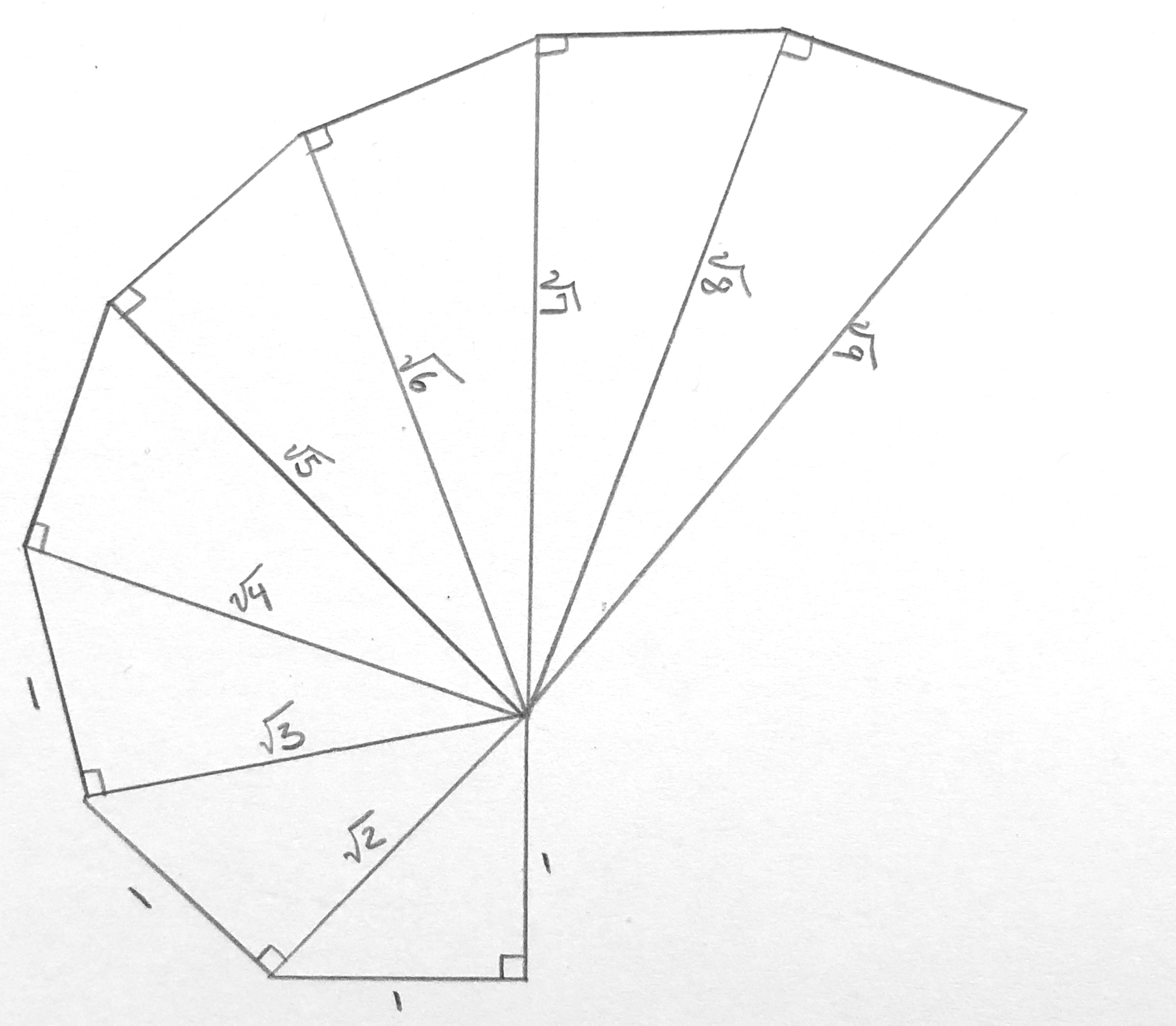
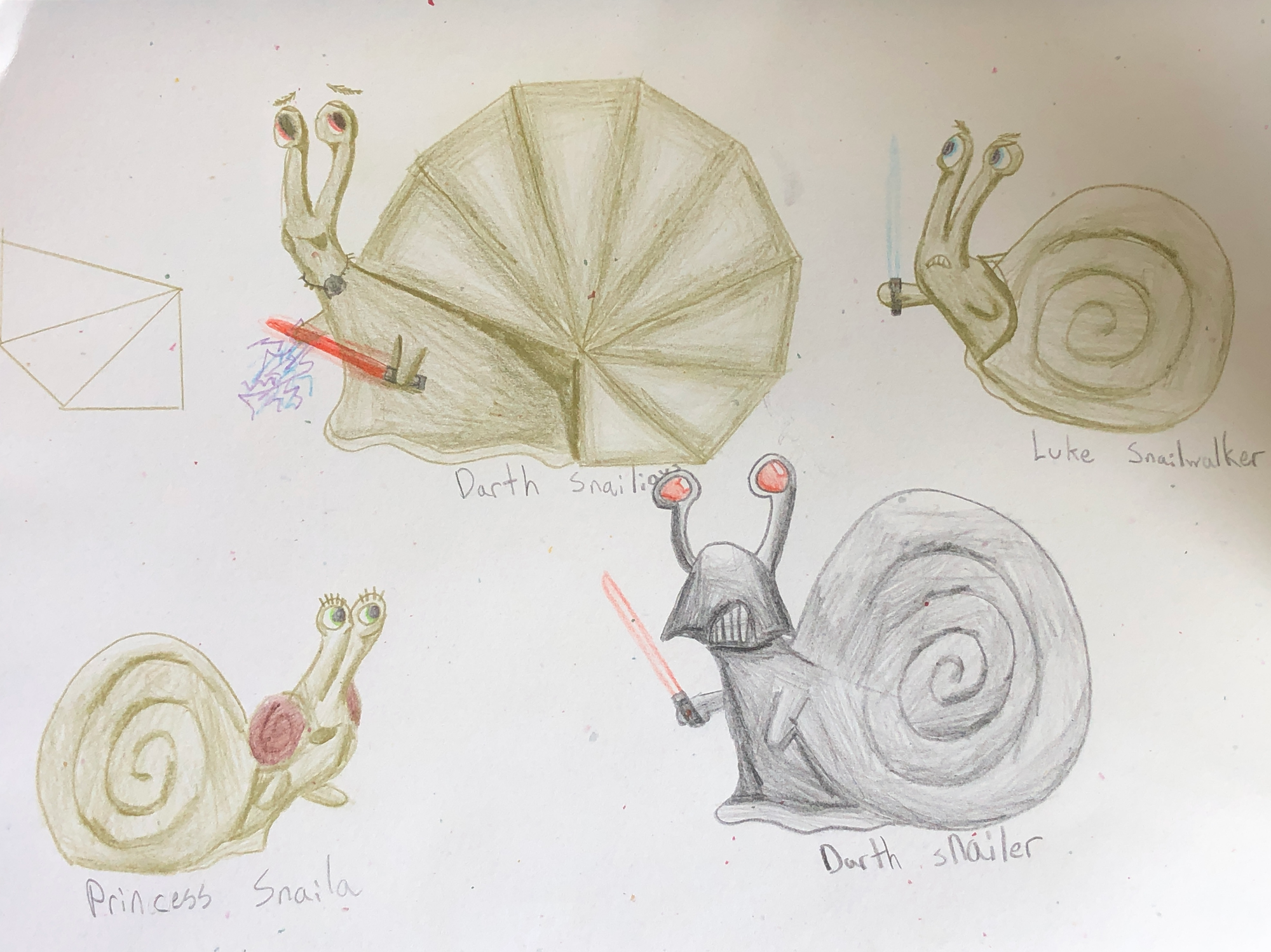
5.) When your done, you can transform your work into a fun sketch:

Possible reflection/discussion questions:
- How does the Pythagorean Theorem apply here? What pattern do the hypotenuses make?
- Can you create a function that would reflect the rate of growth for the hypotenuses?
- There are so many ways to say “right angle” – can you say it three other ways?
- Can you create an algorithm for making these spirals?

Member discussion