Apollonian Gaskets are a creative way to play with circles, fractals, and mindfulness in math. Students can cut out circles and place them within circles or practice their drafting skills with a compass and ruler. The idea is to draw a large circle and then fit smaller and smaller circles inside as closely as possible (tangent circles). For a great resource on gaskets, click here. For the theorem behind them click here (Descartes’ Theorem). This is a great time to review circle geometry. For middle and high school students, learning Descartes’ Theorem can be a fun. I have found that learners’ desire to be exact in their art has lead them to want to learn the math. However, these sketches need not be perfect; just have fun.

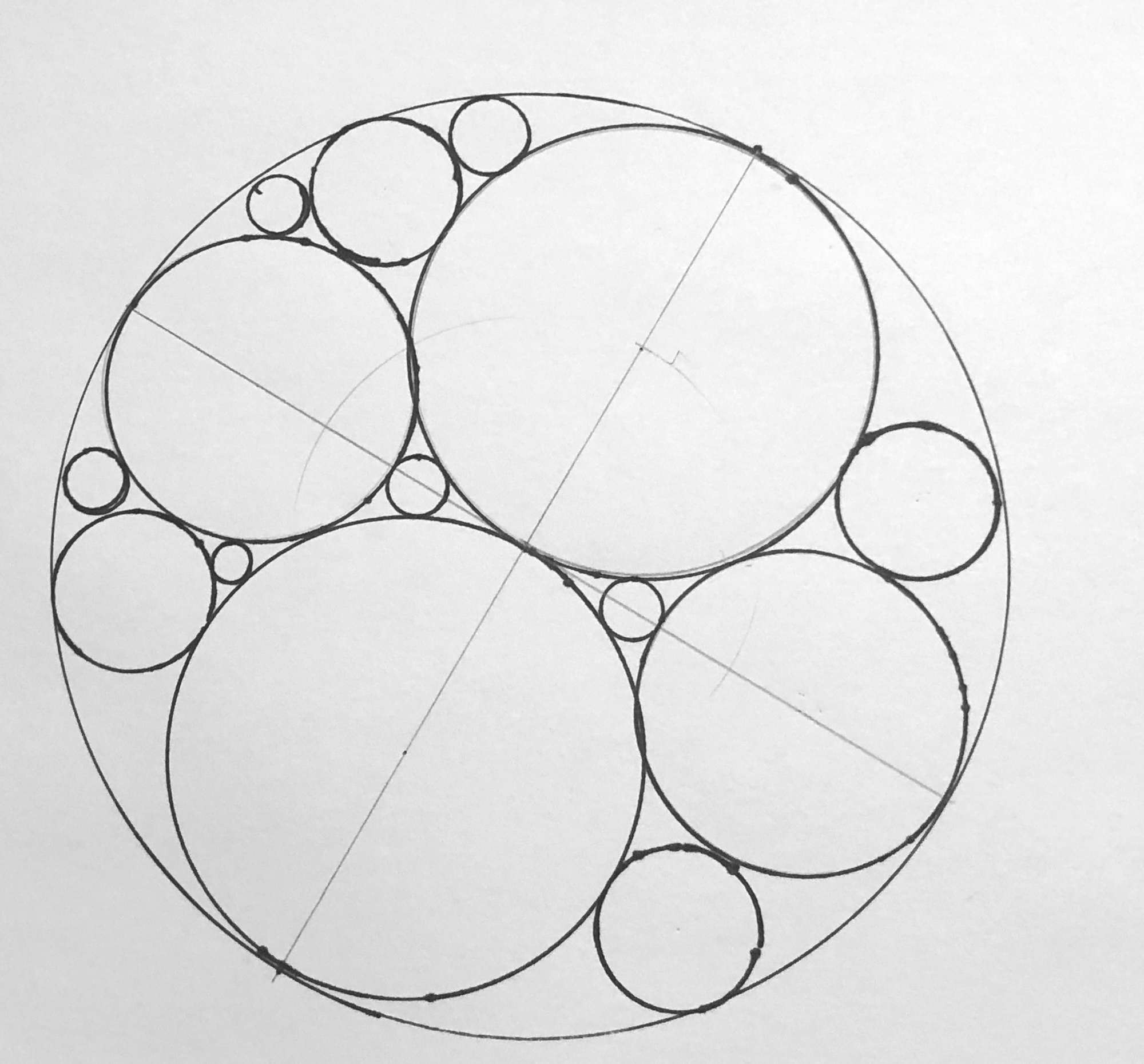
Step 1 – Draw a circle with a compass. Mark the center and sketch a diameter line. It is nice to use pencil and ink for these steps to be able to erase some lines and ink in your circles.

Step 2 – Add marks on the diameter that divide it into fouths. Draw two circles that have a diameter of half of your original circle by placing your compass center at the 1/4th and 3/4ths marks.

Step 3 – Draws circles that fit in the largest two spaces, (1/3 of the radius of the original). Once you set your compass to 1/3 the size of the original circle, zero in on the center of the next circle by using the perpendicular line to the original diameter and moving the compass around until it only touches the outer circle and two inner circles.

Step 4 – If you want to be exact, then you need to use Descartes’ theorem to calculate the size of each circle to proceed. You can also use a circle template or stencil set to eyeball tangent circles. The idea is to continue to fill in the spaces with more and more tangent circles. The sketch below is just approximated for a “quick sketch” and not done with the precision of Descartes’ Theorem.

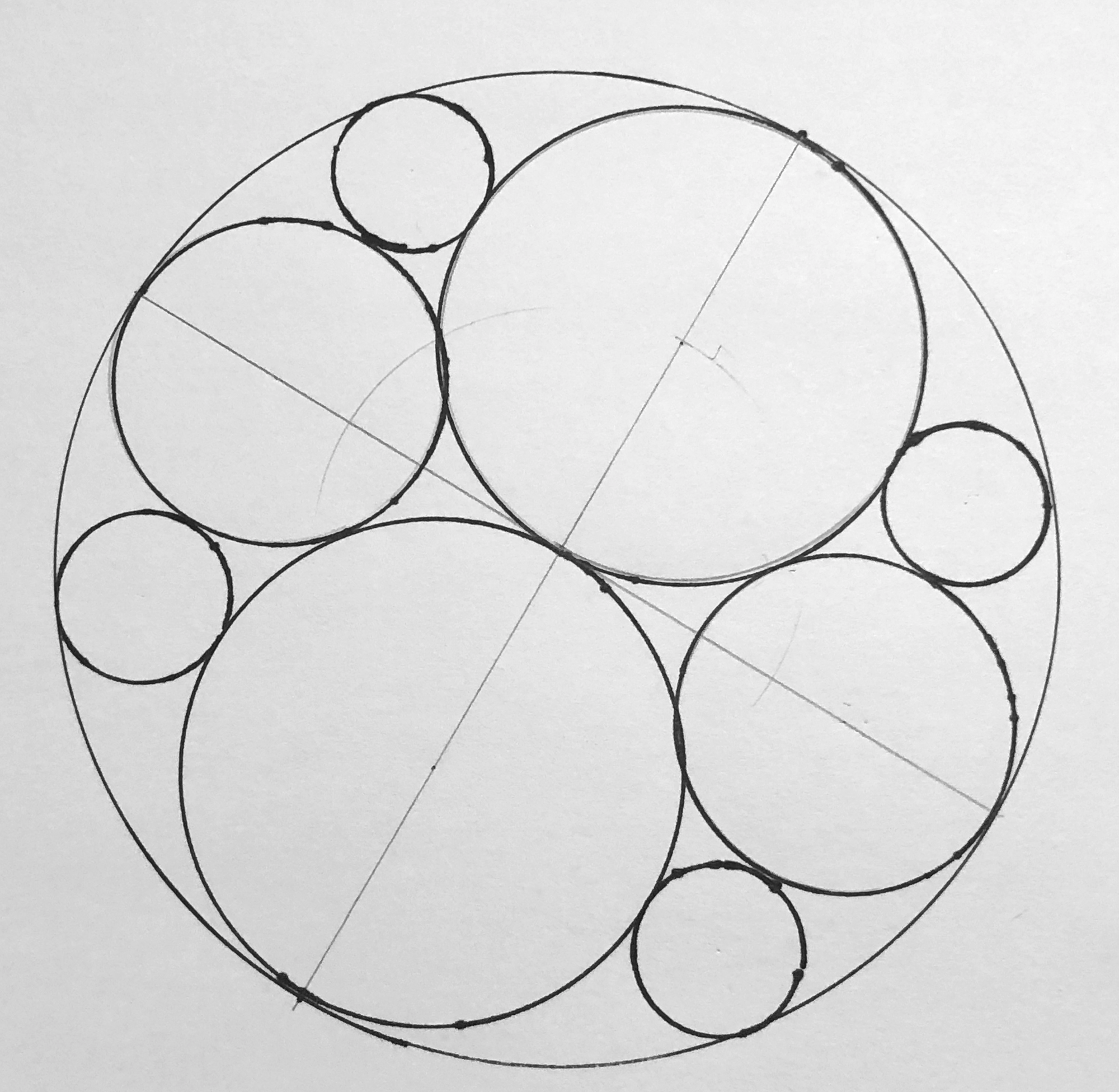
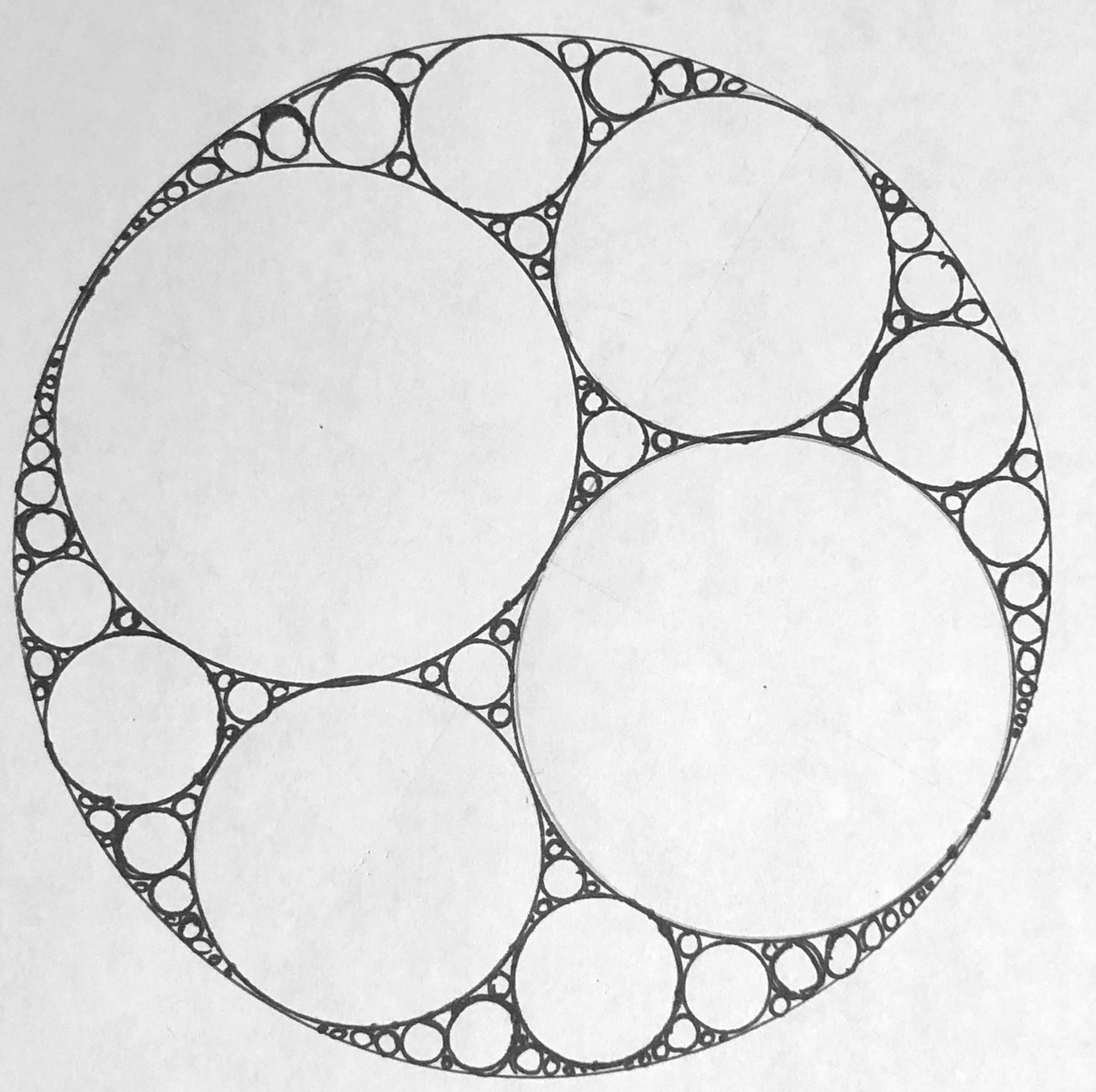
Before writing this entry, I played with cutting an Apollonian Gasket from acrylic. Here is my design for a math toy. The svg file is here (keep in mind that tolerances and resizing may be needed).

• 

• 

• 

• 

• 

• 

• 

• 

•