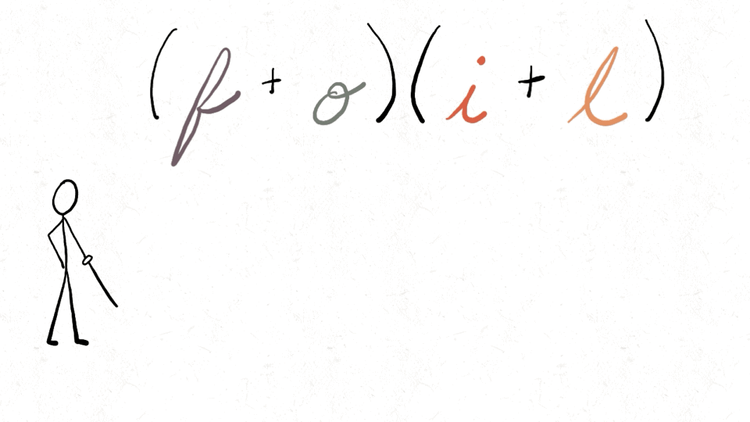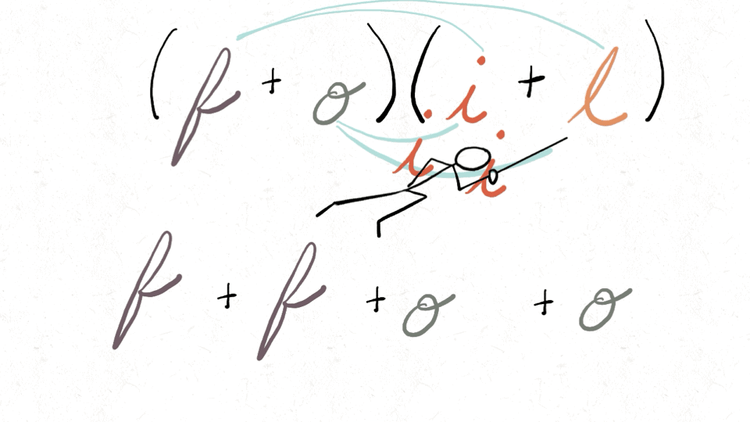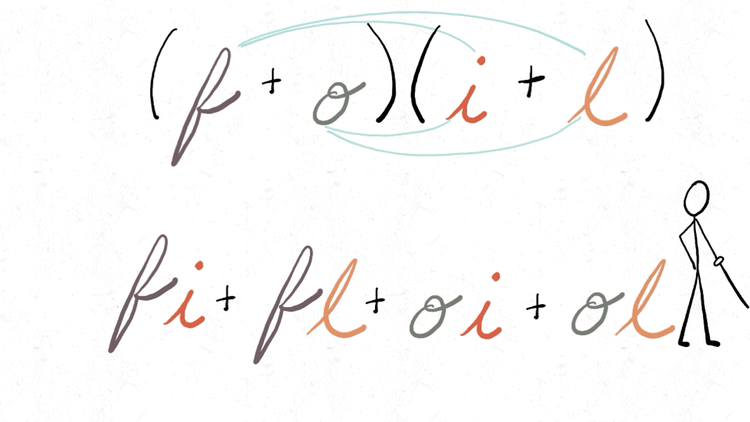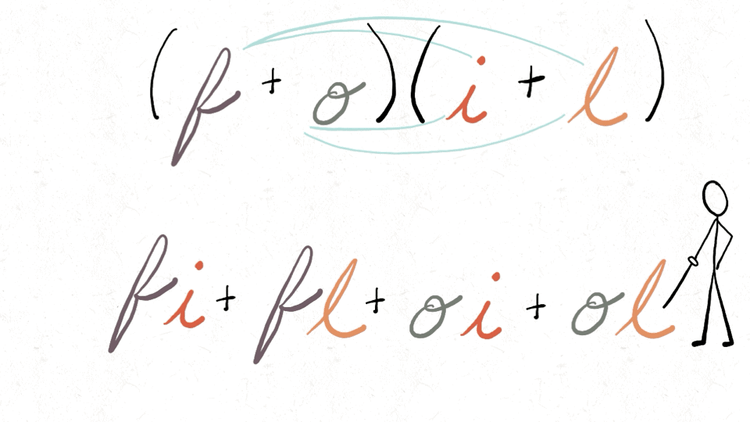11
Nov
Gross-Beak
I got side tracked when thinking about the next math bird in a series and thought “I’m long overdue for a kitty comic.” Dozen=12 and Gross=144
doodle
10
Sep
Get Ready for Mathober!
This year’s Mathober pieces will be posted here. Last year I posted prompts for the first year of Mathober when I wanted to do some daily doodles with no strings attached. The activity was a lot of fun. There were some some great pieces from John Golden and Foldster on Twitter. Prompts this year hav
1 min read
24
Oct
The Point? Dimensions
“The Point of Evolution” started as a Mathober doodle and led to this GIF. Dimensions are fun – what do you see? what do you notice? Side Note: I talk about dimensions when covering combining like terms. One analogy – A 3D banana can’t combine with a 2D banana (or whatever noun seems to go […]
1 min read
25
Sep
From the Void
Hexagon and parametric spiral play. I find myself doodling with code lately more than with my pen. I have one more scripting algebra post, but feel like I have a much larger library for a pre-calc set of activities. Thoughts? The GIF is too large for this site or twitter, so I stashed it on […]
16
Sep
Expanded
With commas: Without commas:
1 min read
13
Sep
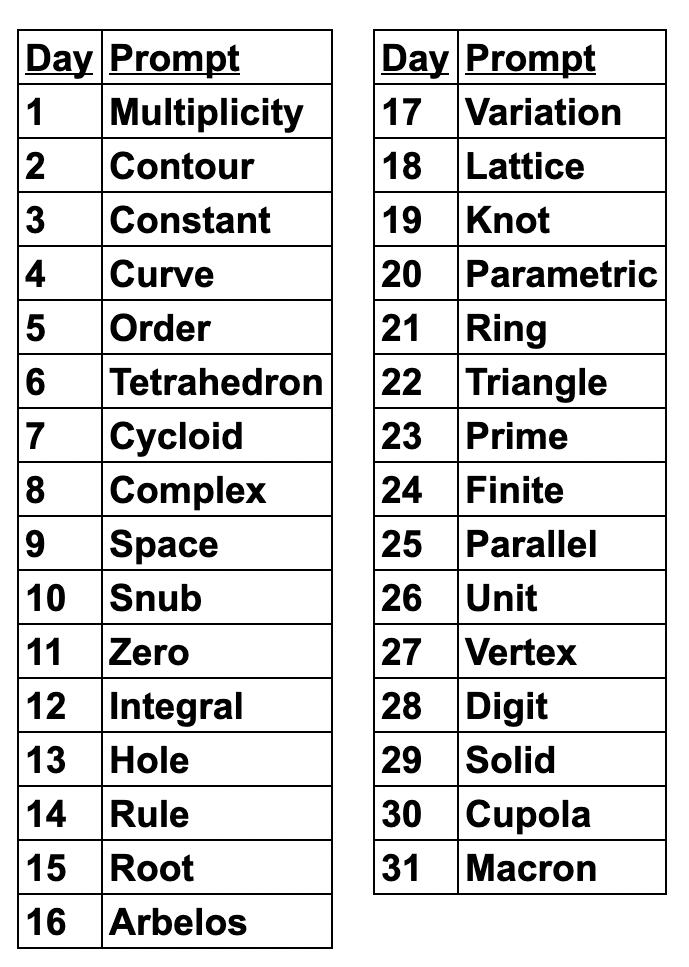
Foiled by a Foil
I couldn’t resist this GIF for my algebra students. Foiling can be such fun!
12
Sep
Moiré GIF: by Opal
My daughter started playing with moiré in procreate after I fiddled with it in a previous post. You know we breathe math in our home. She wanted to share:
09
Sep
Parallel to a Parabola
I received a question today about what curve is parallel to a parabola. I sat for a minute and realized that it wasn’t another parabola. It required parametric equations (at least if you wanted to keep it simple). That of course lead to code: See the Pen jOqzMJb by Sophia (@fractalkitty) on CodePen.
1 min read
05
Sep
Menger Sponge Cat in Space
High res: Low res:
1 min read
02
Sep
Hex-a-Sierpinski
So I doodled and was pleasantly surprised when Sierpinski-like triangles formed. I am sure that a million people have discovered this before me, but I felt like I found a magic portal. And that lead to coding (of which is currently a mess, and I will post later). And one more version:
1 min read