Space-Pigeonholes Imagined
The Pigeonhole Principle merged with the contemplation of black holes today. I envisioned Fractal Kitty at the whiteboard with this one, but went without the kitty today – enjoy.
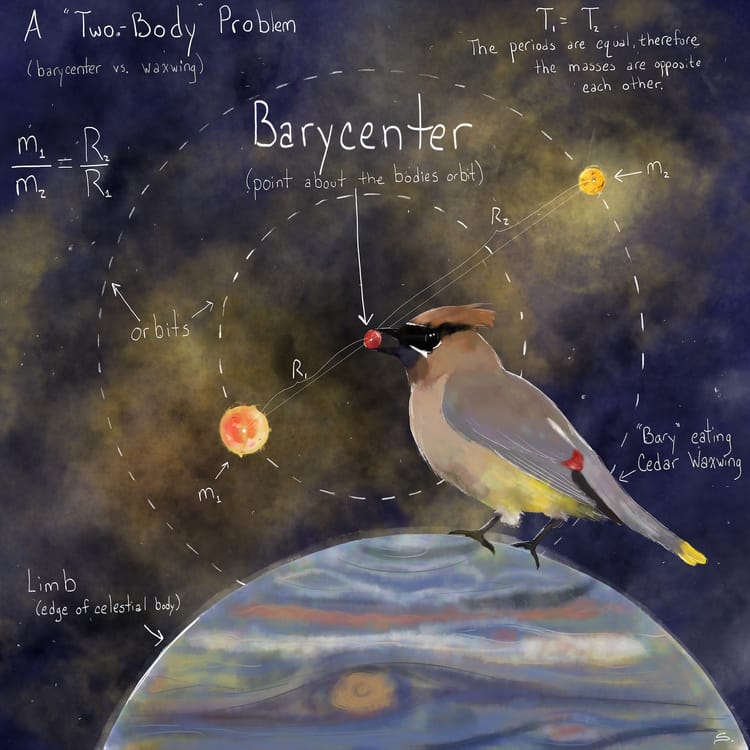
“Two-Body” Problem: Barycenter vs Waxwing
After watching the neighborhood waxwings consume their fill of berries prior to moving on, I pondered a different kind of a two-body problem:
Week 44: Conics, Orbits, and Projectile Motion
You don’t have to be in high school math to play with conics, orbits, and projectile motion. This week (or month) learners can play with projectile motion, orbits, and conics sections with the activities below: 1.) Slicing cones Learners can mold cones with clay and slice to see the possible shapes.
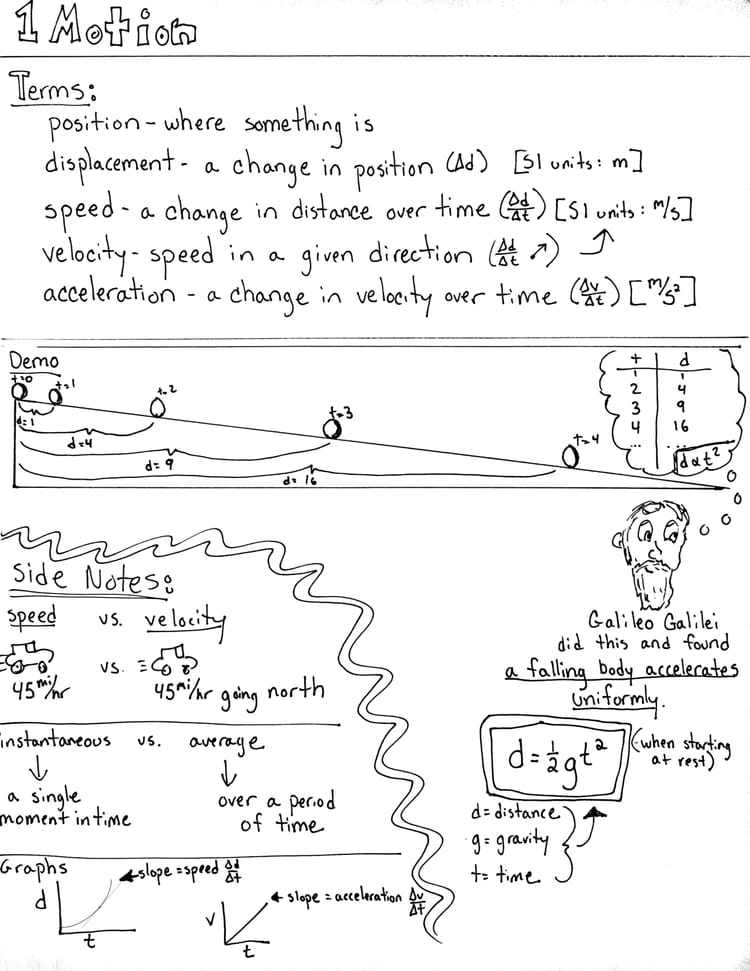
Week 12: Galileo and Gravity
This week we are going to take a look at applied math. Learners will be given a ramp (this can be a ruler), a ball that fits on the ramp, measurement device (ruler) and a timer. With these instruments learners can investigate the relationship between distance and time as the ball rolls down the ramp