String Art Presentation
I put these slides together for the Seattle Math Jam 1/18/2021 and thought I’d share them here. I have investigated string art with many of my middle school groups and have had so much fun finding patterns. This slide deck was put together with some extra toys for small group investigations. Code li
Week 22: Tessellations – Paper Method
This week we will do tessellations that fit together through translation (moving without rotation). We will look at reflection and rotation in other weeks. There are a few different ways to do this, but we will use the paper method today. I always start the class by talking about what different kind
Week 19: Math Haiku
Poetry forms are like a puzzles. You have to take the words you want to say and rearrange them, find synonyms, and reformulate them until they can fit in a form. This problem solving is so similar in math. One of the first forms to play with is the Haiku. It is a three line […]
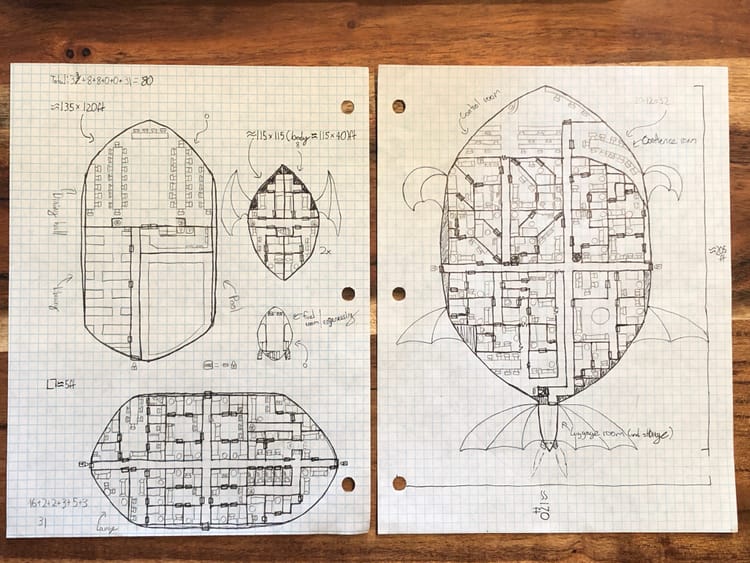
Week 18: Castles, Maps and Spaceships – Let’s Draft
This week learners can dive deep into their imaginary worlds (or real world inventions). The project this week is to create a map, castle, spacecraft or invention. The math focus will be on developing a sense of scale. Younger learners may practice scale with proportions in their drawings. Older lea
Week 1: Embroider Curves with Lines
Welcome to 52 weeks of math! I will be posting a new activity every Wednesday for 52 weeks of hands-on math. Week 1 is one of my favorites – drawing with thread. In this activity, learners will play with their rulers (or thread) to create curves with lines. The idea is to have students draw […]