Week 31: Angle Inquiry

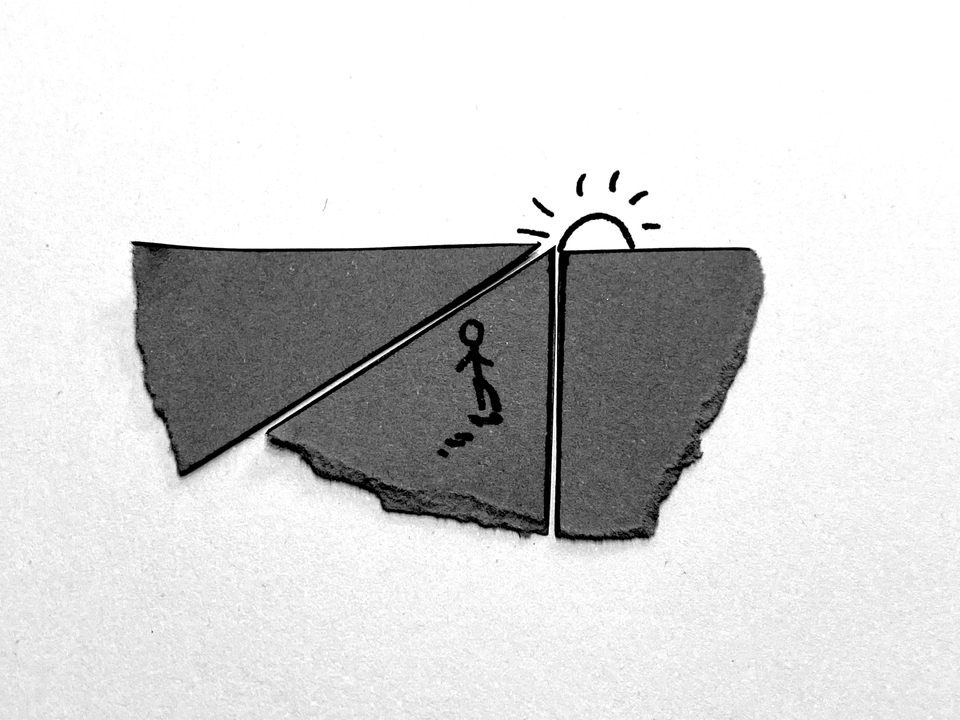
Sometimes the simplest things have wonder hidden within. This week, learners can play with the angles of polygons. How many degrees are in a triangle? In a quadrilateral? In a hexagon? Is there a pattern?

Here is a warm-up activity:

Draw a triangle (any triangle), and cut it out.

Next, rip the corners off:

Now, here is the fun part… put the pointy angles together. What do you get? Try it with lots of triangles and see if you always get a straight line. Rather than lecturing or telling learners that triangles have 180 degrees (or pi radians), let them discover. They can even create art ( I like to make my angles into perspective path doodles.)

Now do the same with a four sided shape. What do you notice? Is it the same for all the ones you can create?

Now do the same with 5, 6 or more sided shapes. There is a rule to be found. Try to discover it if you don’t know. I will put the rule at the bottom of this post.

I did this twice last week with virtual classrooms through the Covid-19 isolation. Students from kindergarten to middle-school ate it up. We used it as a warm up activity (10-15 minutes) prior to doing some loop-doodle math and/or other activities.

and

the

rule

is

stated

right

below:

The rule for simple polygons is that for n sides there are 180(n-2) degrees. Or you add 180 degrees every time you add a side.